Satuan Pendidikan        :   SMP ALAZHAR 1 BANDAR LAMPUNG

Mata Pelajaran              :   Matematika

Kelas / Semester            :   VIII (Delapan) / 2

Materi                             :   Lingkaran

Alokasi Waktu               :  20 JP (@40 menit)

💚💙💛💜"Agama tanpa ilmu pengetahuan adalah buta. Dan ilmu pengetahuan tanpa agama adalah lumpuh" 💓💓💜

Doa Diawaktu pagi Hari

اَللَّهُمَّ إِنِّيْ أَسْأَلُكَ عِلْمًا نَافِعًا، وَرِزْقًا طَيِّبًا، وَعَمَلاً مُتَقَبَّلاً

Allahumma inni as aluka ‘ilman naafi’aa wa rizqan toyyibaa wa ‘amalan mutaqabbalaa

 

“Ya Allah, sungguh aku memohon kepada Mu ilmu yang manfaat, rizki yang baik dan amal yang diterima.” (HR. Ibnu As-Sunni dan Ibnu Majah).

 Assalamu'alaikum Wr Wb.

Sudah Sholat dhuha belum? 👐👐👐

Ibu  berharap kalian selalu istiqomah dalam melaksanakan dhuha dan ibadah wajib lainnya.

Marilah kita selalu bersyukur kehadirat Alloh SWT, yang telah memberikan kita segala yang kita butuhkan. dengan selalu ibadah kita tunjukan rasa syukur kita. 

Anak anak hari ini kita masih belajar tentang  

Kompetensi Dasar

3.7      Menentukan hubungan sudut pusat, panjang busur dan luas juring

 Tujuan Pembelajaran : 

Setelah mengikuti proses pembelajaran, peserta didik dapat

1. Mengetahui hubungan antara sudut pusat dengan sudut keliling yang menghadap busur sama

2 

Hubungan Sudut Pusat, Panjang Busur, Luas Juring, dan Luas Tembereng

Pernahkah Anda melihat orang bermain tolak peluru? Kalau belum pernah melihatnya coba perhatikan gambar di bawah ini!

Gambar di atas merupakan orang yang mau melempar peluru. Tahukah Anda bagaimana bentuk lapangan permainan tolak peluru? Gambar A di bawah ini merupakan gambar bentuk lapangan tolak peluru.

Gambar A

Jika dilihat secara mendetail pada lingkaran (titik A) maka gambar lapangan tolak peluru seperti gambar B di bawah ini.

Gambar B

Dapatkah Anda menghitungnya berapa panjang busur yang dibentk oleh sudut 45 pada Gambar B? Sekarang perhatikan Gambar A, titik A sama seperti gambar B. Jika jarak anak A dan anak B sejauh 100 m, dapatkah Anda hitung berapa panjang busur (garis lengkung) yang dibentuk oleh anak B dan anak C?

Untuk menjawab soal tersebut Anda harus paham dengan konsep keliling lingkaran, sudut pusat, dan panjang busur serta hubungannya.

 

Sudut pusat adalah sudut yang dibentuk oleh dua jari-jari yang berpotongan pada pusat lingkaran. Pada gambar di bawah, sudut AOB = α adalah sudut pusat lingkaran. Garis lengkung AB disebut busur AB dan daerah arsiran OAB disebut juring OAB. Pada pembahasan kali ini, kita akan mempelajari hubungan antara sudut pusat, panjang busur, dan luas juring pada sebuah lingkaran.

 

Hubungan antara sudut pusat, panjang busur, dan luas juring adalah sebagai berikut.

Jadi, panjang busur dan luas juring pada suatu lingkaran berbanding lurus dengan besar sudut pusatnya. 

 

Sekarang perhatikan Gambar di atas tersebut. Dari gambar tersebut diperoleh

Sekarang, misalkan ∠ COD = satu putaran penuh = 360° maka keliling lingkaran = 2πr, dan luas lingkaran = πr² dengan r jari-jari, akan tampak seperti Gambar di atas, sehingga diperoleh

 

Dengan demikian, diperoleh rumus panjang busur AB, luas juring AB, dan luas tembereng AB pada Gambar di atas adalah

panjang busur AB = (α/360°) x 2πr

luas juring OAB = (α/360°) x πr²

luas tembereng AB = luas juring OAB – luas Δ AOB.

Contoh Soal 

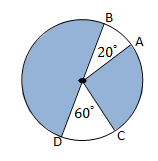
Perhatikan gambar berikut.

Jika panjang busur AB = 45 cm, maka berapakah panjang busur CD?

Penyelesaian:

Tugas!!

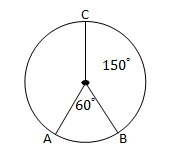
1. Pada gambar berikut, jika luas juring AOB adalah 40 cm2, maka berapakah luas juring BOC?

2. Panjang jari-jari sebuah lingkaran dengan pusat O adalah 5 cm. Titik P dan Q terletak pada lingkaran. Jika panjang busur PQ = 6,28 cm, hitunglah luas juring POQ.

Tugas!!!

1. Selesaikan tugas diatas

2. Silahkan dikumpul dengan cara japri lewat WA ke Ibu